Propiedades métricas de rectas y planos

Comenzamos hablando del cálculo de ángulos, podemos encontrar un ángulo entre dos rectas, dos planos y una recta y un plano. Para ello solo es necesario calcular el ángulo formado por el respectivo vector director o respectivo vector normal, excepto en el caso de una recta y un plano, donde tendrás que hacer el arcoseno.

Otra propiedad sería el cálculo de proyecciones, hemos visto como podemos calcular la proyección de un punto en un plano o en una recta, y la proyección de una recta en un plano.

Uno de los usos más habituales de las proyecciones es en cartografía. Dado que La Tierra es una esfera, para representar su geografía se utilizan proyecciones como la de Mercator, que consisten en proyectar el globo terráqueo sobre un cilindro. Posteriormente, realizando un corte vertical de este cilindro se obtiene una superficie plana al que llamamos mapa. Casi todos los mapas emplean proyecciones de este tipo, aunque puede haber variaciones en la forma de construir la proyección.

Por último vemos el cálculo de distancias en geometría, hemos visto cómo hallar la distancia entre dos puntos, de un punto a un plano, entre dos planos, de una recta a un plano, de un punto a una recta y entre dos rectas. Para todo esto es necesario tener un dominio de los conceptos básicos explicados en temas anteriores y una buena capacidad espacial, para así poder relacionar conceptos y saber aplicar de forma práctica todas las fórmulas. 

En general la geometría es indispensable en nuestro día a día. Sin geometría, no podríamos construir cosas, fabricar cosas o practicar deportes con mucho éxito. La geometría no solo hace las cosas posibles en la vida cotidiana, sino que también las hace más fáciles al proporcionarnos una ciencia exacta para calcular las medidas de formas, ángulos y áreas. 

Rectas y planos en el espacio

 Para estudiar las rectas en el espacio debemos conocer las diferentes formas de expresarla, sus diferentes ecuaciones: 

Utilizaremos sobre todo la ecuación parametrica, la continua y la implícita.

Para sacar un punto de una recta debemos de dar valores, y para sacar un vector debemos hacer el determinante de una matriz en la que en la primera fila incluyamos i,j,k y en las dos siguientes los numeros que multiplican a cada incognita de cada ecuación respectivamente.

Por otra parte tenemos el plano, podemos montar su ecuación general con un punto y dos vectores. Haciendo el determinante igualado a 0 de la ecuacion que tendrá: en las dos primeras columnas las coordenadas de los dos vectores respectivamente, y en la última columna pondremos x,y,z, restando a cada término cada coordenada del punto en orden. 

Podemos hayar el vector normal de un plano (perpendicular), dándole de coordenadas los números que múltiplican a cada coordenada (x,y,z) en su ecuación.

Sabiendo estos conceptos básicos, a partir de aquí podemos calcular las posiciones relativas en el espacio de dos rectas, dos o tres planos, y una recta y un plano.

A esto podemos encontrarle inumerables aplicaciones en la vida real, la geometría en general es campo que nos sirve para cosas tan sencillas como puede ser  diseñar un folleto o encajar una pieza de cerámica en determinado espacio, así como calcular el volumen de agua o entender correctamente un plano o un mapa. Dominar los conceptos básicos no ayuda, por ejemplo, en la compresión de planos bidimensionales sobre objetos tridimensionales.

En la arquitectura concretamente es sumamente importante dominar el campo geométrico, ya que es indispensable en la construcción de edificios.

Vectores en el espacio

El origen de los vectores se remonta al siglo XIX, con el estudio de Hamilton de los cuaterniones. En esta época comenzó el interés por el espacio y las formas de estudiarlo, y para ello se requería utilizar las matemáticas. Se dividió el estudio del espacio en una parte escalar y otra parte vectorial, que en un principio se trataron de estudiar conjuntamente, hasta darse cuenta de que podía hacerse por separado, en esto participó el físico estadounidense Gibbs que fue quien acuñó el término vector por primera vez. La utilización de vectores le ha sido muy útil a la física y es una de sus herramientas fundamentales.

Se comenzaron por estudiar los vectores en un plano de tres dimensiones, es decir, con tres coordenadas. Las coordenadas se expresan según la base ortonormal del espacio vectorial que es (i,j,k), que vienen de los cuaterniones mencionados anteriormente, por lo que cada coordenada irá seguida de la letra correspondiente respectivamente.

Las coordenadas nos indican la dirección del vector, y con ellas podemos calcular también el módulo del vector, que es lo mismo que su longitud en unidades. Para ello debemos hacer la raíz cuadrada de la suma de cada una de las coordenadas al cuadrado:

Podemos hacer varias operaciones entre diferentes vectores, la más básica es el producto escalar, que no es más que la suma de los resultados de multiplicar cada coordenada de uno por la equivalente del otro. De esta manera el producto escalar de un vector u (1,2,3) y otro vector w (0,2,1), sería igual a 7. Es interesante saber también que esta operación nos sirve para saber si dos vectores son perpendiculares, pues si lo son su producto escalar será 0. Con estas operaciones comenzamos a introducirnos en el estudio algebraico de los mismos.

Sabiendo esto, podemos hallar ya el ángulo que forman dos vectores, ya que no es más que hacer el arcocoseno de la división del producto escalar de estos entre la multiplicación de sus módulos.

También podemos hallar la proyección de uno sobre otro, ya que la fórmula es la misma que la descrita anteriormente, solo que en valor absoluto y cambiando el denominador por únicamente el módulo del vector sobre el que se quiere proyectar.

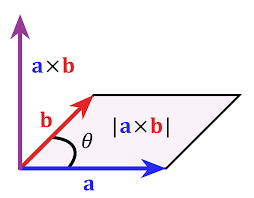
Con los conocimientos del tema de matrices podemos también calcular el producto vectorial de dos vectores. Para ello debemos hacer una matriz que tenga la primera fila con las coordenadas base (i,j,k), la segunda debe tener las coordenadas de uno de los vectores en orden, y así la tercera fila con las coordenadas del otro vector. A continuación hacemos el determinante de la respectiva matriz ya ya estaría. El vector resultante es perpendicular a los otros dos.

Haciendo el módulo de este vector resultante hayamos el área del paralelogramo que tiene de lados los dos vectores con los que hemos realizado el producto vectorial.

Así como dos vectores pueden formar un paralelogramo, 3 forman un paralelepípedo, y para hallar el volumen de este podemos hacer el producto mixto de 3 vectores, que no es más que hacer un matriz de 3x3, que tiene como filas las coordenadas de cada vector en orden, un vector por fila, y hacer el determinante de esta matriz. Importante el valor absoluto en la operación.

Las aplicaciones de los vectores están sobre todo destinadas a la física, ya que sirven para representar cualquier tipo de magnitud vectorial, como por ejemplo la fuera gravitatoria de un cuerpo o el campo electromagnético. En la astronomía el estudio de estos es indispensable.

Sistemas de ecuaciones

 ¿Qué es un sistema de ecuaciones?

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas, de las cuales que queremos obtener su solución común a todas ellas.

Clasificación de sistemas de ecuaciones

Se dice que dos sistemas son equivalentes si son compatibles con las mismas soluciones o si ambos son incompatibles.

Se dice que un sistema es homogéneo cuando todos los términos independientes son nulos.

Historia de los sistemas de ecuaciones

Desde la antigüedad se utilizaron las matrices para resolver los sistemas de ecuaciones lineales, habiendo registros de éstos en Egipto y China mucho antes de que dicho conocimiento pasase a Occidente. 

En el siglo XVII Leibniz desarrolla la teoría de determinantes para facilitar la resolución de ecuaciones lineales, y en 1750 Cramer presenta la que será conocida como la regla de Cramer, con esta se podrá expresar el resultado de los sistemas en términos de determinantes.

En el siglo XIX el matemático Eugène Rouché enuncia el teorema de Rouché- Frobenius, el cual es posteriormente probado por el alemán Ferdinand Frobenius (de ahí el nombre), y permite calcular el número de soluciones que tendrá un sistema en función de el rango de su matriz.

Discutir un sistema

Para discutir un sistema de ecuaciones lo más recomendable es utilizar el teorema de Rouché-Frobenius. El cual dice lo siguiente:

• Si el rg(A)=rg(A*)=nº de incógnitas---------> Sistema compatible determinado (única solución real)

Determinantes

 ¿Qué es un determinante?

Un determinante es el número real que se asocia a una matriz A (también es el volumen del paralelepípedo conformado por tres vectores no coplanarios). Para calcularlo es necesario sumar todos todos los n! productos posibles de n elementos (orden de la matriz) de forma que en cada producto haya un elemento de cada fila y uno de cada columna. Se denota como det(A).

Breve historia

Los determinantes llegaron a Europa desde China en el s. XVI, donde ya se conocían desde hace cientos de años y se utilizaban para resolver sistemas de ecuaciones lineales. Desde entonces, numerosos matemáticos como Leibniz, Cardano o Maclaurin hicieron grandes aportaciones a su desarrollo.

Tipos de determinantes:

• De orden 2

Estos son los más sencillos de calcular, se multiplican en cruz los 4 elementos y se resta un producto menos el otro.

• De orden 3

Para calcular los determinantes de matrices de orden 3 se recomienda seguir la regla de Sarrus (imagen), la cual indica el orden de las operaciones y su signo.

• De orden mayor a 3 (debajo)

Menores de una matriz

Son los determinantes resultantes de eliminar cualquier número de filas o columnas de una matriz de cualquier dimensión, por tanto, si deseamos calcular un determinante de una matriz no cuadrada debemos utilizar este método. También emplearemos este método para calcular el determinante de una matriz de orden >3.

Adjunto de una matriz

El adjunto de una matriz es su menor complementario multiplicado por (-1)^i+j Siendo 'i' el número que ocupa la fila excluida del menor y 'j' el de la columna. De esta manera, si la suma de ambos valores es par, el valor del menor complementario será positivo y si es impar, negativo.

Rango de una matriz

El rango de una matriz rang(A) es el número de filas o columnas linealmente independientes. Este lo podemos calcular por el método de Gauss o por determinantes. Si tomamos la última opción, es necesario tomar menores de la matriz cuyo rango queremos estudiar, si uno de ellos no es 0, significará que el rango de la matriz cuadrada es su orden. Por otro lado, si todos ellos dan 0, significará que el rango de la matriz es menor a su orden. 

En el caso de que no sea cuadrada, si en la matriz A existe un menor de orden p distinto de 0 y todos los menores de orden p+1 son nulos el rang(A) =p.

Matriz inversa (por determinantes)

Gracias a los determinantes, existe otro método para calcular la matriz inversa a otra, además del de Gauss (ver matrices). Cuya fórmula es la siguiente:

Aplicaciones de los determinantes

Los determinantes son utilizados en sectores como: 

• Hotelería
• Alimentación y nutrición
• Ingenierías

Matrices

 ¿Qué es una matriz?

Una matriz es un conjunto bidimensional de números símbolos o expresiones (elementos), los cuales se ordenan en filas y columnas. A una matriz con m filas y n columnas se la denomina matriz m x n. El término 'matriz' fue acuñado por el matemático inglés Joseph Sylvester en 1848, aunque se sabe que éstas habían sido utilizadas con anterioridad.

Origen e historia de las matrices

Recientemente se ha descubierto que las matrices y los determinantes ya eran conocidos en la Antigua China hace miles de años, habiendo registros en la literatura de su uso hacia el año 200 a.C. aproximadamente, como se puede observar en la imagen inferior.

Posteriormente, el conocimiento pasó a India y luego al mundo árabe, donde se conocían como ''cuadrados mágicos'', en torno al s.VII d.C. En el 983 aparecieron los primeros cuadrados mágicos de orden 5 y 6 en Bagdad. 

En Europa el conocimiento llegó con el Renacimiento y Modernismo (s. XV - XVII), el matemático alemán Leibniz las trata en su obra sobre los determinantes aplicados a la resolución de sistemas de ecuaciones lineales publicada en 1693.

La siguiente gran aportación a las matrices la hizo Gabriel Cramer en 1750, formulando la que se conocería como la regla de Cramer (ver en sistemas de ecuaciones).

En el s. XIX Carl Friedrich Gauss (imagen) y Wilhelm Jordan desarrollan el método de Gauss-Jordan, un algoritmo mediante el cual se consigue obtener una matriz triangular superior a partir de cualquier matriz y posteriormente una matriz diagonal. Se utiliza para calcular la matriz inversa a otra y resolver sistemas de ecuaciones principalmente.

Años más tarde, Arthur Cayley introdujo la multiplicación de matrices la notación matricial y, junto al matemático Hamilton, elaboró un teorema en que se afirma que cualquier matriz cuadrada es solución de un polinomio.

En el pasado siglo se llevaron a cabo numerosas aportaciones al calculo matricial, entre los que destacan Ferdinand Georg Frobenius (método de Rouché-Frobenius), Olga- Taussky Todd, John von Neuman y Werner Heisenberg. Este último tuvo especial relevancia, ya que mediante el calculo matricial, formula el preludio de lo que se conocerá como mecánica cuántica. 

Método de Gauss-Jordan aplicado para hacer la inversa de una matriz:

Dividimos la matriz inicial en dos bloques, la de la izquierda es la matriz original (A) y la de la derecha la matriz identidad (I). A continuación, operamos las filas (F), con el objetivo de cambiar ambos bloques de lugar, teniendo a la matriz I a la izquierda. Cuando lo hallamos conseguido, la matriz que nos quede a la derecha será la matriz inversa (A^-1).

Aplicaciones de las matrices:

Las matrices tienen múltiples aplicaciones, no solo en matemáticas, también en física y en las ciencias sociales. Algunas de éstas son:

1. Matemáticas

• Resolver sistemas de ecuaciones
• Relacionar datos
• Calculo vectorial (ver entrada)

2. Física

• Transformaciones de Lorenz
• Mecánica cuántica

3. Ciencias sociales

En Geografía y Economía se utilizan para elaborar tablas de doble entrada con diversas finalidades:

• Indicar distancias
• Predecir las demandas de producción
• Interpretar relaciones económicas entre distintos sectores de producción