Vectores en el espacio

El origen de los vectores se remonta al siglo XIX, con el estudio de Hamilton de los cuaterniones. En esta época comenzó el interés por el espacio y las formas de estudiarlo, y para ello se requería utilizar las matemáticas. Se dividió el estudio del espacio en una parte escalar y otra parte vectorial, que en un principio se trataron de estudiar conjuntamente, hasta darse cuenta de que podía hacerse por separado, en esto participó el físico estadounidense Gibbs que fue quien acuñó el término vector por primera vez. La utilización de vectores le ha sido muy útil a la física y es una de sus herramientas fundamentales.

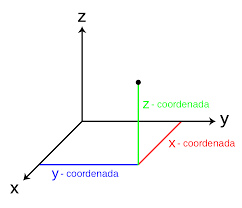
Se comenzaron por estudiar los vectores en un plano de tres dimensiones, es decir, con tres coordenadas. Las coordenadas se expresan según la base ortonormal del espacio vectorial que es (i,j,k), que vienen de los cuaterniones mencionados anteriormente, por lo que cada coordenada irá seguida de la letra correspondiente respectivamente.

Las coordenadas nos indican la dirección del vector, y con ellas podemos calcular también el módulo del vector, que es lo mismo que su longitud en unidades. Para ello debemos hacer la raíz cuadrada de la suma de cada una de las coordenadas al cuadrado:

Podemos hacer varias operaciones entre diferentes vectores, la más básica es el producto escalar, que no es más que la suma de los resultados de multiplicar cada coordenada de uno por la equivalente del otro. De esta manera el producto escalar de un vector u (1,2,3) y otro vector w (0,2,1), sería igual a 7. Es interesante saber también que esta operación nos sirve para saber si dos vectores son perpendiculares, pues si lo son su producto escalar será 0. Con estas operaciones comenzamos a introducirnos en el estudio algebraico de los mismos.

Sabiendo esto, podemos hallar ya el ángulo que forman dos vectores, ya que no es más que hacer el arcocoseno de la división del producto escalar de estos entre la multiplicación de sus módulos.

También podemos hallar la proyección de uno sobre otro, ya que la fórmula es la misma que la descrita anteriormente, solo que en valor absoluto y cambiando el denominador por únicamente el módulo del vector sobre el que se quiere proyectar.

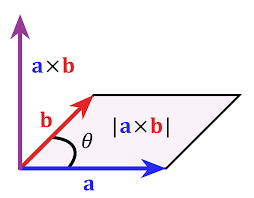
Con los conocimientos del tema de matrices podemos también calcular el producto vectorial de dos vectores. Para ello debemos hacer una matriz que tenga la primera fila con las coordenadas base (i,j,k), la segunda debe tener las coordenadas de uno de los vectores en orden, y así la tercera fila con las coordenadas del otro vector. A continuación hacemos el determinante de la respectiva matriz ya ya estaría. El vector resultante es perpendicular a los otros dos.

Haciendo el módulo de este vector resultante hayamos el área del paralelogramo que tiene de lados los dos vectores con los que hemos realizado el producto vectorial.

Así como dos vectores pueden formar un paralelogramo, 3 forman un paralelepípedo, y para hallar el volumen de este podemos hacer el producto mixto de 3 vectores, que no es más que hacer un matriz de 3x3, que tiene como filas las coordenadas de cada vector en orden, un vector por fila, y hacer el determinante de esta matriz. Importante el valor absoluto en la operación.

Las aplicaciones de los vectores están sobre todo destinadas a la física, ya que sirven para representar cualquier tipo de magnitud vectorial, como por ejemplo la fuera gravitatoria de un cuerpo o el campo electromagnético. En la astronomía el estudio de estos es indispensable.