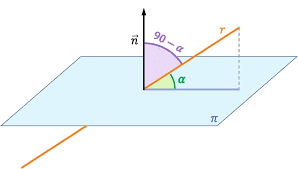
Comenzamos hablando del cálculo de ángulos, podemos encontrar un ángulo entre dos rectas, dos planos y una recta y un plano. Para ello solo es necesario calcular el ángulo formado por el respectivo vector director o respectivo vector normal, excepto en el caso de una recta y un plano, donde tendrás que hacer el arcoseno.
Otra propiedad sería el cálculo de proyecciones, hemos visto como podemos calcular la proyección de un punto en un plano o en una recta, y la proyección de una recta en un plano.
Uno de los usos más habituales de las proyecciones es en cartografía. Dado que La Tierra es una esfera, para representar su geografía se utilizan proyecciones como la de Mercator, que consisten en proyectar el globo terráqueo sobre un cilindro. Posteriormente, realizando un corte vertical de este cilindro se obtiene una superficie plana al que llamamos mapa. Casi todos los mapas emplean proyecciones de este tipo, aunque puede haber variaciones en la forma de construir la proyección.
Por último vemos el cálculo de distancias en geometría, hemos visto cómo hallar la distancia entre dos puntos, de un punto a un plano, entre dos planos, de una recta a un plano, de un punto a una recta y entre dos rectas. Para todo esto es necesario tener un dominio de los conceptos básicos explicados en temas anteriores y una buena capacidad espacial, para así poder relacionar conceptos y saber aplicar de forma práctica todas las fórmulas.
En general la geometría es indispensable en nuestro día a día. Sin geometría, no podríamos construir cosas, fabricar cosas o practicar deportes con mucho éxito. La geometría no solo hace las cosas posibles en la vida cotidiana, sino que también las hace más fáciles al proporcionarnos una ciencia exacta para calcular las medidas de formas, ángulos y áreas.



No hay comentarios:
Publicar un comentario